P-Q-Formel Aufgaben und P-Q-Formel Übungen zum Lösen Quadratischer Gleichungen

Die pq-Formel ist eine Lösungsformel für quadratische Gleichungen.

Dabei müsst ihr beachten dass die quadratische Gleichung bereits in der richtigen Form ist:

Warum müssen wir quadatische Gleichungen überhaupt lösen können?

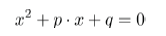
Quadratische Gleichungen begegnen uns in der Physik, Natur und an vielen anderen stellen. Das Lösen einer quadratischen Gleichung können wir immer anschaulich auf die Bestimmung von Nullstellen einer Parabel zurückführen. Wenn in einer Problemstellung eine quadratische Funktion auftritt, müssen wir auch fast immer eine quadratische Gleichung lösen. Z.B. beim schrägen Wurf in der Physik sprechen wir von einer "Wurfparabel" oder der "Bahnkurve". In der Architektur und im Brückenbau begegnen uns ebenso häufig Parabeln, deren Nullstellen wir bestimmen müssen.

Hier ein Beispiel einer quadratischen Funktion und dem Schaubild der dazu gehörigen Parabel:

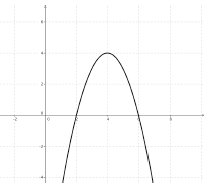
Zu dieser Parabel gehört die Funktionsgleichung:

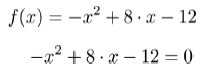
Bei dieser Parabel können wir glücklicherweise die Nullstellen sogar ablesen.

In der folgenden Rechnung können wir damit direkt prüfen, ob das berechnete Ergebnis richtig ist.

Ihr seht die beiden Nullstellen bei x = 2 und x = 6.

Wie lösen wir nun eine quadratische Gleichung?

Nehmen wir unsere Beispielfunktion mit der quadratischen Gleichung zur Bestimmung der Nullstellen:

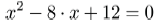
Hier die Lösungsschritte - ziel ist es, die quadratsche Gleichung in eine Form zu bringen, in der wir x nur noch in einer Klammer stehen haben, wie wir es von den binomischen Formeln kennen. Diese Vorgehensweise nennt man quadratische Ergänung.

Wir erhalten eine vereinfachte Gleichung, die wir durch Wurzelziehen lösen können:

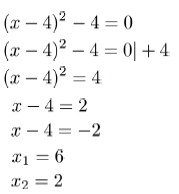
Die Gleichung (x-4) zum Quadrat gleich 4 können wir intuitiv oder durch Ziehen der Wurzel lösen.

In diesem Beispiel haben wir die Technik der quadratischen Ergänzung kennen gelernt.

Das haben wir gemacht, um eine binomische Formel in unserer Gleichung zu erhalten.

Jetzt wollen wir eine allgemeine Gleichung mit den Parametern p und q auf die gleiche Weise lösen.

Herleitung einer Lösung die zur pq-Formel führt:

Wir ergänzen zunächst allgemein mit einem Term, der uns eine binomische Formel als Teil der Gleichung liefert:

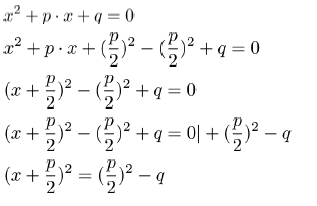
Nachdem wir den quadratischen Teil auf einer Seite alleine stehen haben, können wir die Wurzel ziehen:

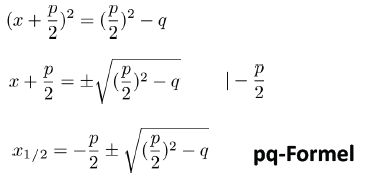
Nachdem wir die Wurzel gezogen haben und nur noch x auf einer Seite steht, erhalten wir die PQ-Formel.

Wir wollen die pq-Formel nun anwenden auf unser Beispiel:

Hierbei ist in unserer Beispielgleichung p = -8 und q = 12.

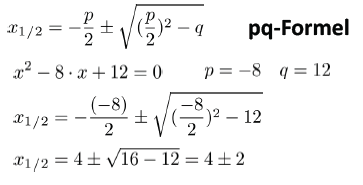
Nach Umformun erhalten wir die Lösungen x = 2 und x = 6, wie wir oben schon aus dem Bild ablesen konnten.

Nicht immer kann man die Lösungen aus einem Bild ablesen.

Stellt sich noch eine  Frage: funktioniert die pq-Formel immer?

Die Antwort lautet: ja und nein.

JA: Wenn man sie richtig interpretieren kann.

NEIN: Da nicht jede quadratische Gleichung lösbar ist.

Es gibt auch quadratische Gleichungen, die keine Lösung haben. Anschaulich betrachtet bedeutet das, dass eine Parabel keine Schnittpunkte mit der x-Achse hat.

Das entscheidende ist der Term unter der Wurzel:

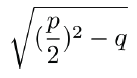
1. Ist dieser Term gleich Null, hat die quadratische Gleichung nur eine Lösung. Die pq-Formel funktioniert und liefert 1 Lösung.

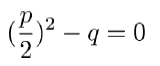
2. Ist dieser Ausdruck größer Null, können wir die Wurzel in der pq-Formel ziehen und wir erhalten 2 Lösungen. Die pq-Formel funktioniert.

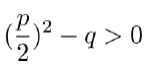
3. Ist dieser Term kleiner Null, dürfen wir keine Wurzel ziehen, die Wurzel ist nicht definiert. Die pq-Formel liefert keine Lösung!

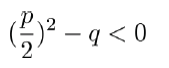
 Alle Schritte als PDF oder als Powerpoint-Folie im Download-Bereich mit online Zugang vorhanden!