Fit fürs Abi in Mathe - Die Basics für aus der Mittelstufe: 150 Seiten Matheaufgaben + ausführliche Lösungen

Ab sofort auch als Einzeldownload verfügbar im Mathefritz-Shop.

Demnächst im Handel als Buch mit Lösungen (280 Seiten komplett, Aufgaben + Lösungen)

Mathematik kann entmutigend wirken, aber mit den richtigen Hilfsmitteln kann sie zum Kinderspiel werden. Wenn du in der Mittelstufe bist und deine mathematischen Fähigkeiten verbessern möchtest, haben wir genau das Richtige für dich. Wir stellen vor: "Basics für die Mittelstufe: 150 Seiten Matheaufgaben mit einfachen Lösungen."

Dieser umfassende Leitfaden soll dir eine solide Grundlage in Mathematik bieten, indem er dir eine breite Palette von Problemen und deren einfache Lösungen präsentiert. Ganz gleich, ob du dich auf eine Prüfung vorbereitest, deine Mathematikkenntnisse auffrischen oder einfach nur neugierig auf neue Konzepte bist, diese sorgfältig zusammengestellte Sammlung von Matheaufgaben wird dir helfen.

Von Algebra über Trigonometrie bis hin zu Parabeln und quadratischen Gleichungen deckt jedes Kapitel ein bestimmtes Thema ab und enthält eine Vielzahl von Aufgaben, die dich herausfordert und beschäftigt. Die Lösungen sind leicht verständlich geschrieben, damit du die Konzepte dahinter verstehst. Die Lösungen befinden sich in einem eigenen Dokument.

Lass dich nicht länger von Mathematik einschüchtern. Mit "Grundlagen für die Mittelstufe: 150 Seiten Matheaufgaben mit einfachen Lösungen" gewinnst du das Selbstvertrauen und die Fähigkeiten, selbst die komplexesten Matheaufgaben zu bewältigen. Machen dich bereit, in Mathe so gut zu sein wie nie zuvor!

Das Buch ist im Handel als Buch noch NICHT erschienen.

Einleitung zum Lösen mathematischer Probleme

Das Lösen mathematischer Probleme erfordert eine systematische Herangehensweise und ein Verständnis für die zugrunde liegenden Konzepte. In dieser Einführung werden wir dir einige bewährte Methoden vorstellen, die dir helfen werden, mathematische Probleme effektiv anzugehen.

Zunächst ist es wichtig, dass du die Aufgabenstellung sorgfältig liest und die gegebenen Informationen identifizierst. Erkenne, was das Problem verlangt und welche Art von Lösung erwartet wird. Wenn nötig, skizziere Diagramme oder visualisiere das Problem, um dir bei der Vorstellung zu helfen.

Ein weiterer wichtiger Schritt ist es, den mathematischen Zusammenhang zu identifizieren. Überlege, welche mathematischen Konzepte und Formeln auf das Problem angewendet werden können. Manchmal erfordert dies auch das Umformen der gegebenen Informationen, um sie in eine geeignete Form zu bringen.

Sobald du den Zusammenhang verstanden hast, kannst du mit der eigentlichen Lösung beginnen. Arbeite schrittweise vor und notiere dir Zwischenergebnisse, um sicherzustellen, dass du auf dem richtigen Weg bist. Überprüfe am Ende deine Lösung, um sicherzustellen, dass sie logisch und korrekt ist.

Indem du diese Schritte befolgst und regelmäßig mathematische Probleme löst, wirst du mit der Zeit immer sicherer und schneller darin werden. Das Üben ist der Schlüssel zum Erfolg in der Mathematik.

Matheaufgaben visuell lösen - Ein Beispiel

hier findest du ein Beispiel aus dem Buch, in dem wir anschaulich das Thema kurz beschreiben, bevor wie viele Aufgaben rechnen. Die Lösungen dazu findest du natürlich in dem dazu gehörigen Lösungsbuch!

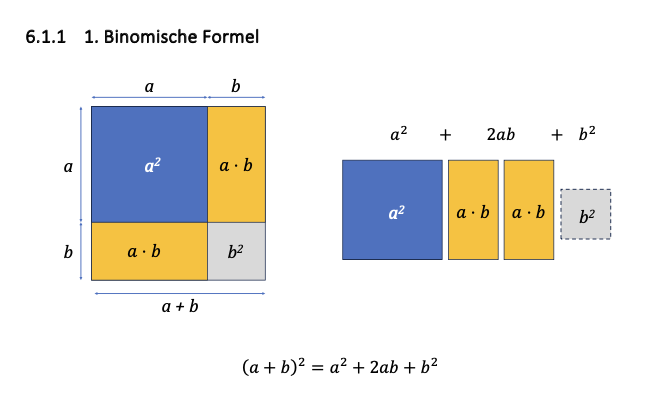
Binomische Formeln anschaulich erklärt.

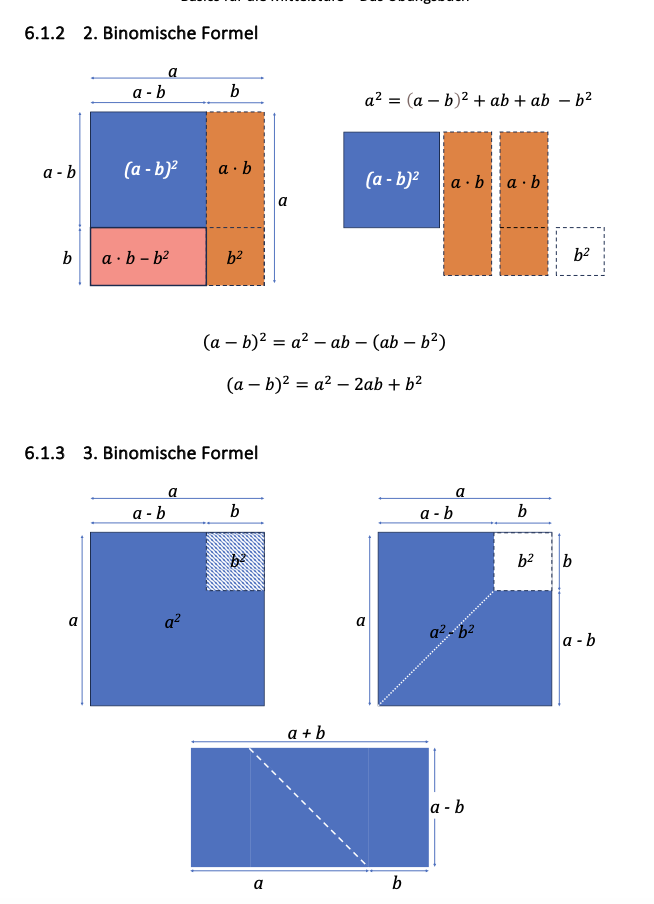
Und dann folgen die Aufgaben:

Die Bedeutung des Übens mathematischer Probleme und Aufgaben

Das Üben mathematischer Probleme ist von entscheidender Bedeutung, um ein tieferes Verständnis für mathematische Konzepte zu entwickeln und die Fähigkeiten zur Problemlösung zu verbessern. Es ermöglicht dir, deine mathematischen Fähigkeiten zu festigen und dich mit verschiedenen Arten von Aufgaben vertraut zu machen.

Durch regelmäßiges Üben verbesserst du nicht nur deine Rechenfertigkeiten, sondern auch deine Fähigkeit, mathematische Probleme zu analysieren und logisch zu denken. Es hilft dir dabei, Muster und Zusammenhänge zu erkennen und komplexe Probleme in kleinere, überschaubare Schritte zu zerlegen.

Das Üben mathematischer Probleme hilft dir auch dabei, deine Fehler zu erkennen und zu korrigieren. Indem du die Lösungen überprüfst und verstehst, warum bestimmte Ansätze richtig oder falsch sind, kannst du deine Denkweise und Herangehensweise verbessern.

Darüber hinaus ermöglicht das Üben mathematischer Probleme eine bessere Vorbereitung auf Prüfungen und Tests. Indem du dich kontinuierlich mit verschiedenen Arten von Aufgaben auseinandersetzt, wirst du selbstbewusster und besser in der Lage sein, mathematische Probleme effektiv zu lösen.

Vorteile der Verwendung von Büchern mit einfachen Lösungen

Die Verwendung von Büchern mit einfachen Lösungen bietet eine Vielzahl von Vorteilen für Schülerinnen und Schüler in der Mittelschule. Diese Bücher sind speziell darauf ausgerichtet, mathematische Konzepte auf eine verständliche und zugängliche Weise zu präsentieren.

Ein großer Vorteil besteht darin, dass die Lösungen in Büchern mit einfachen Lösungen oft schrittweise erklärt werden. Dies ermöglicht es den Schülern, den Lösungsweg nachzuvollziehen und die zugrunde liegenden Konzepte besser zu verstehen. Dadurch wird das Lernen effektiver und nachhaltiger.

Ein weiterer Vorteil von Büchern mit einfachen Lösungen ist, dass sie eine Vielzahl von Aufgaben unterschiedlicher Schwierigkeitsgrade enthalten. Dies ermöglicht es den Schülern, ihr Wissen und ihre Fähigkeiten schrittweise zu erweitern und sich an zunehmend anspruchsvollere Aufgaben heranzutasten.

Darüber hinaus können Bücher mit einfachen Lösungen als Selbstlernwerkzeuge verwendet werden. Schülerinnen und Schüler können eigenständig arbeiten und ihre Fortschritte überprüfen, ohne auf die Hilfe eines Lehrers angewiesen zu sein. Dies fördert die Unabhängigkeit und das Selbstvertrauen in den eigenen mathematischen Fähigkeiten.

Insgesamt bieten Bücher mit einfachen Lösungen eine solide Grundlage für das Erlernen und Vertiefen von mathematischen Kenntnissen. Sie sind eine wertvolle Ergänzung zum regulären Unterricht und können dazu beitragen, dass Schülerinnen und Schüler besser in Mathe werden.

Wie man das richtige Mathebuch auswählt

Die Auswahl des richtigen Mathebuchs ist entscheidend, um das Beste aus deiner Lernerfahrung herauszuholen. Hier sind einige Tipps, die dir bei der Auswahl des richtigen Mathebuchs helfen werden:

1. Überprüfe den Inhalt: Schau dir das Inhaltsverzeichnis des Buches an und überprüfe, ob es die mathematischen Themen abdeckt, die du lernen möchtest. Stelle sicher, dass das Buch sowohl Grundlagen als auch fortgeschrittene Konzepte behandelt, um sicherzustellen, dass es deinen Bedürfnissen entspricht.
2. Berücksichtige dein Niveau: Wähle ein Buch, das auf deinem aktuellen mathematischen Kenntnisstand basiert. Wenn du bereits fortgeschrittene Mathematik beherrschst, wähle ein Buch, das Herausforderungen auf diesem Niveau bietet. Wenn du jedoch noch grundlegende Konzepte festigen möchtest, wähle ein Buch, das für Anfänger geeignet ist.
3. Lies Rezensionen: Überprüfe, ob das Buch positive Bewertungen und Rezensionen von anderen Schülern oder Lehrern erhalten hat. Dies kann dir helfen, die Qualität des Buches einzuschätzen und zu entscheiden, ob es deinen Anforderungen entspricht.
4. Betrachte den Stil des Buches: Jeder hat einen anderen Lernstil. Überlege, ob du von einem Buch profitieren würdest, das viele Beispiele und Übungen enthält oder ob du lieber ein Buch mit klarer und prägnanter Erklärung bevorzugst.
5. Preis-Leistungs-Verhältnis: Berücksichtige dein Budget und vergleiche die Preise verschiedener Bücher. Berücksichtige jedoch auch die Qualität und den Wert, den das Buch bietet. Manchmal ist es besser, etwas mehr Geld für ein hochwertiges Buch auszugeben, das dir langfristig mehr Nutzen bringt.

Indem du diese Tipps berücksichtigst und verschiedene Bücher vergleichst, wirst du in der Lage sein, das richtige Mathebuch für deine Bedürfnisse auszuwählen und deine Lernerfahrung zu optimieren. Eine große Auswahl an Büchern findest du auch bei Amazon.de .

Übersicht über unser 150-seitiges Matheaufgabenbuch

Das 150-seitige Matheaufgabenbuch "Grundlagen für die Mittelschule" bietet eine umfassende Sammlung von mathematischen Problemen, die auf verschiedene Themenbereiche abzielen. Hier ist eine Übersicht über die verschiedenen Kapitel und Themen, die im Buch behandelt werden:

1. Terme
2. Gleichungen / Ungleichungen
3. Lineare Funktionen
4. Lineare Gleichungssysteme
5. Binomische Formeln
6. Quadratische Terme faktorisieren
7. Bruchterme
8. Wurzeln
9. Satz des Pythagoras
10. Potenzen
11. Parabeln und quadratische Funktionen
12. Quadratische Gleichungen
13. Trigonometrie
14. Der Kreis
15. 3D Körper berechnen

Diese Kapitel sind nur eine Vorschau auf die Vielfalt der Themen, die im Buch abgedeckt werden. Jedes Kapitel enthält eine Vielzahl von Aufgaben, die dich herausfordern und motivieren werden.

Tipps zum Visualisieren von Matheaufgaben

In unserem Mathe Buch Basics für die Mittelstufe haben wir viele mathematische Probleme und Aufgaben mit Hilfe von GeoGebra visualisiert. Dadurch kannst du die Problemstellung viel besser verstehen. Das haben wir z.B. auf unserer GeoGebra-Seite bereitgestellt. Schau einfach einmal vorbei!

Hier ein Beispiel aus dem buch und eine direkte Anwendung bei GeoGebra zum Thema Pythagoras und Höhensatz:

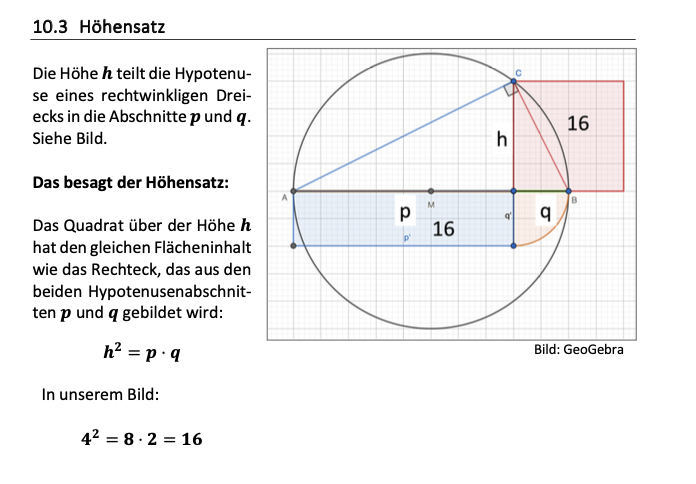
Und dazu passend die interaktive Übung bei GeoGebra: (auch über diesen Link: https://www.geogebra.org/m/mbh7pwhy  ) 

Klicke den Punkt C an und verschiebe ihn im Kreis!

Tipps zum effektiven Lösen von Matheaufgaben

Das Lösen von Matheaufgaben erfordert nicht nur mathematisches Wissen, sondern auch effektive Strategien und Herangehensweisen. Hier sind einige Tipps, die dir helfen werden, Matheaufgaben effektiver anzugehen:

1. Verstehe das Problem: Lies die Aufgabenstellung sorgfältig und identifiziere die gegebenen Informationen sowie das gewünschte Ergebnis. Stelle sicher, dass du das Problem vollständig verstehst, bevor du mit der Lösung beginnst.
2. Skizziere oder visualisiere das Problem: Manchmal hilft es, ein Diagramm oder eine Skizze des Problems zu erstellen, um es besser zu verstehen. Visualisierung kann dir helfen, Zusammenhänge zu erkennen und die Probleme in überschaubare Schritte zu zerlegen.
3. Suche nach Mustern und Zusammenhängen: Oft gibt es in mathematischen Problemen Muster oder Zusammenhänge, die dir bei der Lösung helfen können. Suche nach diesen Mustern und nutze sie, um den Lösungsweg zu finden.
4. Arbeite schrittweise: Teile das Problem in kleinere Schritte auf und notiere dir Zwischenergebnisse. Dies ermöglicht es dir, den Überblick zu behalten und sicherzustellen, dass du auf dem richtigen Weg bist.
5. Überprüfe deine Lösung: Gehe am Ende noch einmal deine Lösung durch und überprüfe, ob sie logisch und korrekt ist. Überprüfe auch, ob deine Lösung dem gegebenen Kontext entspricht.

Indem du diese Tipps befolgst und regelmäßig Matheaufgaben löst, wirst du deine Fähigkeiten zur Problemlösung verbessern und selbstbewusster in der Mathematik werden.

Häufige Fehler beim Lösen von Matheaufgaben vermeiden

Beim Lösen von Matheaufgaben können einige häufige Fehler auftreten, die zu falschen Lösungen oder Missverständnissen führen können. Hier sind einige häufige Fehler, die du vermeiden solltest:

1. Unvollständiges Lesen der Aufgabenstellung: Es ist wichtig, die Aufgabenstellung vollständig zu lesen und alle gegebenen Informationen zu identifizieren. Unvollständiges Lesen kann dazu führen, dass wichtige Informationen übersehen werden, was zu falschen Lösungen führt.
2. Fehlerhafte Anwendung von Formeln: Achte darauf, dass du die richtigen Formeln und Konzepte auf das gegebene Problem anwendest. Überprüfe deine Berechnungen sorgfältig, um sicherzustellen, dass du die richtigen Schritte durchführst.
3. Fehlende Zwischenschritte: Wenn du komplexe Probleme löst, ist es wichtig, viele Zwischenschritte zu gehen und diese sauber zu notieren. Nur so kannst du den Weg zur richtigen Lösung gut finden und auch dokumentieren.