Bruchrechnen einfach erklärt
Bruchrechnung verstehen - Kürzen, Erweitern, Addition, Multiplikation, Division, Rechnen mit Brüchen
Auf dieser Seite lernst du über die Bruchrechnung:
- Was ist ein Bruch, wie schreibt man einen Bruch
- Brüche anschaulich und in Bruchschreibweise
- Was versteht man unter Kürzen und Erweitern eines Bruchs
- Brüche addieren, subtrahieren, multiplizieren und dividieren
- Brüche in Dezimalbrüche oder Prozentwerte umwandeln
- Viele Aufgaben und Klassenarbeiten zur Bruchrechnung und Beispiele
- Viele Lernvideos zum Thema Bruchrechnung - aus unserem Youtube Kanal!
Schreibweise eines Bruchs:
Drei Achtel schreibt man z.B. so:
$ \frac{3}{8} = \frac{Zaehler}{Nenner}$
Die Zahl auf dem Bruchstrich nennt man Zähler, die Zahl unter dem Bruchstrich Nenner!
Einfache Bruchteile kann man sich immer auch anschaulich als Bild vorstellen. In userem Beispiel
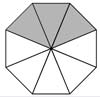
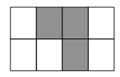
zwei Varianten der bildlichen Darstellung von drei Achtel.
Bruchteil bedeutet, dass wir einen Teil von einem Ganzen betrachten. Der Anteil der betrachtet wird, steht im Zähler (und wird damit quasi "gezählt"), die Anteile des Ganzen stehen im Nenner.
In unserem Beispiel haben wir somit 3 Teile von insgesamt 8 und das schreibt man als drei Achtel als Bruch: $ \frac{3}{8}$.
Weitere Beispiele von einfachen Bruchteilen:
- zwei Fünftel: zwei Anteile von insgesamt 5 als Bruch: $ \frac{3}{8}$
- ein Zwölftel: ein Anteil von insgesamt 12 als Bruch:$\frac{1}{12}$
- drei Siebtel: drei Anteile von insgesamt 7 als Bruch: $\frac{3}{7}$
- vier Neuntel: vier Anteile von insgesamt 9 als Bruch:$ \frac{4}{9}$
Stammbruch - Definition
Ein Bruch mit dem Wert 1 im Zähler wird manchmal auch Stammbruch genannt!
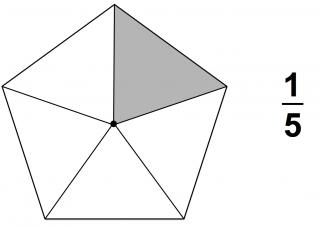
Die folgenden Brüche sind Stammbrüche: $\frac{1}{2} \:, \frac{1}{3} \:, \frac{1}{5} \:, \frac{1}{8} \:, \frac{1}{10} $
Mit online Zugang alle Seiten OHNE WERBUNG!
Brüche anschaulich und in Bruchschreibweise
Der erste und einfachste Schritt beim Erlernen der Bruchrechnung sind die beiden Aufgaben:
- Erkennen von Bruchteilen aus einem Bild
- Markieren eines gegebenen Bruchteils in einem Bild
Diese Aufgaben sind ein umfangreicher Bereich in dem Übungsheft zur einfachen Bruchrechnung.
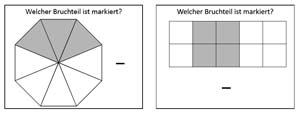
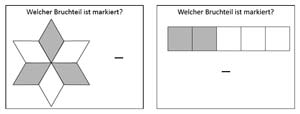
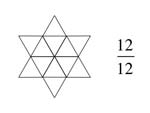
Beispielaufgaben - Erkenne die Bruchteile und gebe Sie an:
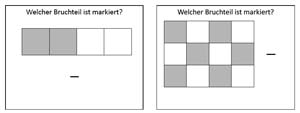
Beispielaufgaben - Markiere die angegebenen Bruchteile im Bild farbig:
a) Markiere die Anteile: $ \frac{2}{5}, \: \frac{4}{5}$
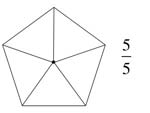
b) Markiere die Anteile farbig: $\frac{1}{6} \:, \frac{5}{6} $
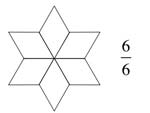
c) Markiere die Anteile farbig: $\frac{5}{12} \:, \frac{3}{4} $
Weitere Aufgaben und Arbeitsblätter zu diesem Thema findet ihr auf der Seite Bruchteile, dort findet ihr auch die Powerpoint-Vorlage für diese Burchteile.
Tipp: die Powerpoint Vorlage für Bruchteile eignet sich besonders fürs Smartboard!
Kürzen eines Bruchs
Anhand des folgenden Bildes erkennt man anschaulich die Funktionsweise des Kürzens eines Bruchs:

Von 18 Teilen insgesamt sind 6 Teile der gleiche Anteil wie 1 Teil von 3 Teilen gesamt.
In der Bruchschreibweise beschreibt der folgende Sachverhalt das Bild:
$ \frac{6}{18} = \frac{1}{3} $
Hier wurde Zähler und Nenner des usprüngichen Bruchs durch 6 geteilt:
$ \frac{6:6}{18:6} = \frac{1}{3}$
Definition Kürzen eines Bruchs:
Unter dem Kürzen eines Bruchs versteht man, den Zähler und Nenner eines Bruchs durch die gleiche Zahl zu dividieren (teilen).
Merke: das Kürzen eines Bruchs vereinfacht lediglich den Bruch, verändert allerdings NICHT seinen Wert!
Regel zur Durchführung des Kürzens:
Zerlege Zähler und Nenner in Faktoren bis es nicht mehr weiter geht. Dann streiche gemeinsame Teiler im Zähler und Nenner durch. die restlichen verbleibenden Faktoren wieder multipliziert ergeben den gekürzten Bruch:
Was genau damit gemeint ist, seht ihr in diesem Beispiel:
$ \frac{6}{18} = \frac{2 \cdot 3}{2 \cdot 3 \cdot 3}=\frac{1}{3} $
Wenn alle Zahlen wie hier im Zähler die 2 und 3 gestrichen werden können, bleibt natürlich die 1 übrig, da jede Zahl das neutrale Element 1 als Faktor enthält!
Aufgaben zur Bruchrechnung - Kürzen
Mit den folgenden Aufgaben kannst du prüfen, ob du das Kürzen eines Bruchs verstanden hast.
1. Aufgabe: Kürze mit der angegebenen Zahl!
a) $\frac{6}{15}$ mit 3
b) $\frac{14}{20}$ mit 2
c) $\frac{8}{12}$ mit 4
d) $\frac{9}{15}$ mit 3
e) $\frac{15}{20}$ mit 5
f) $\frac{21}{49}$ mit 7
g) $\frac{24}{32}$ mit 8
h) $\frac{9}{21}$ mit 3
i) $\frac{10}{25}$ mit 5
j) $\frac{35}{50}$ mit 7
k) $\frac{28}{35}$ mit 7
l) $\frac{19}{38}$ mit 19
m) $\frac{16}{40}$ mit 4
n) $\frac{144}{240}$ mit 12
o) $\frac{60}{72}$ mit 6
p) $\frac{90}{105}$ mit 15
Viele weitere solcher Aufgaben zur Bruchrechnung findet ihr im Übungsheft einfache Bruchrechnung!
2. Aufgabe: Kürze vollständig - d.h. bis es nicht mehr weiter geht!
a) $\frac{16}{20}$
b) $\frac{12}{26}$
c) $\frac{81}{90}$
d) $\frac{10}{15}$
e) $\frac{15}{25}$
f) $\frac{21}{35}$
g) $\frac{24}{36}$
h) $\frac{81}{90}$
i) $\frac{10}{40}$
j) $\frac{45}{50}$
k) $\frac{65}{115}$
l) $\frac{17}{51}$
m) $\frac{36}{72}$
n) $\frac{150}{165}$
o) $\frac{60}{75}$
p) $\frac{63}{81}$
Erweitern eines Bruchs
Anschaulich bedeutet das Erweitern eines Bruchs, dass man die Gesamtanzahl der Stücke vergößert.
Stell dir vor, du ißt 1 Stück Kuchen und der Kuchen war zunächst nur in 4 Stücke aufgeteilt. Dann hast du $\frac{1}{4}$ also in Worten: ein Viertel davon gegessen.
Wäre der gleiche Kuchen in 8 Stücke geschnitten gewesen, dann müßtest du jetzt 2 Stücke essen.
Das sieht in der Grafik so aus:
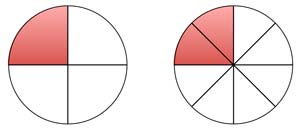
In der Bruchschreibweise ist das : $ \frac{1}{4}=\frac{2}{8} $
Was haben wir in der Bruchschreibweise gemacht? Wir haben Zähler und Nenner mit 2 multipliziert. Das kann man verallgemeinern und erhält die Definition für das Erweitern eines Bruchs:
Definition Erweitern eines Bruchs
Unter dem Erweitern eines Bruchs versteht man, Zähler und Nenner eines Bruchs mit der gleichen Zahl zu multiplizieren.
Merke: das Erweitern eines Bruchs verändert lediglich den Bruch, verändert allerdings NICHT seinen Wert!
Wozu braucht man das Erweitern?
Brüche muss man erweitern, wenn man sie z.B. addieren möchte. Das erkläre ich im nächsten Schritt.
Zunächst einmal einige Beispielaufgaben, um Brüche korrekt zu erweitern!
Aufgaben zur Bruchrechnung - Erweitern
Mit den folgenden Aufgaben kannst du prüfen, ob du das Erweitern eines Bruchs verstanden hast.
1. Aufgabe: erweitere mit der angegebenen Zahl!
a) $\frac{1}{5}$ mit 3
b) $\frac{2}{7}$ mit 2
c) $\frac{1}{3}$ mit 4
d) $\frac{2}{9}$ mit 3
e) $\frac{10}{11}$ mit 5
f) $\frac{7}{9}$ mit 5
g) $\frac{11}{12}$ mit 4
h) $\frac{3}{20}$ mit 7
i) $\frac{1}{25}$ mit 4
j) $\frac{7}{12}$ mit 3
k) $\frac{8}{125}$ mit 4
l) $\frac{3}{5}$ mit 20
m) $\frac{1}{30}$ mit 3
n) $\frac{10}{25}$ mit 8
o) $\frac{6}{8}$ mit 2
p) $\frac{3}{10}$ mit 10
Viele weitere solcher Aufgaben zur Bruchrechnung findet ihr auch im Übungsheft einfache Bruchrechnung!
Gemischte Aufgaben - Kürzen und Erweitern
Wenn du Kürzen und Erweitern verstanden hast, kannst du auch die folgenden Aufgaben lösen:
1. Aufgabe: Ergänze jeweils den fehlenden Zähler oder Nenner!
a) $\frac{1}{4} = \frac{}{12}$
b) $\frac{}{3} = \frac{6}{9}$
c) $\frac{2}{5} = \frac{}{25}$
d) $\frac{5}{12} = \frac{}{60}$
e) $\frac{2}{3} = \frac{8}{}$
f) $\frac{7}{15} = \frac{}{45}$
Viele weitere Aufgaben dieses Typs zur Bruchrechnung findet ihr auch im Übungsheft einfache Bruchrechnung!
Gemischte Bruchschreibweise
Umwandlung von gemischter Schreibweise in reine Bruchschreibweise und umgekehrt
dieses Kapitel wird noch erstellt!
Brüche addieren und subtrahieren
So addiert oder subtrahiert man Brüche / Definition
Zwei oder mehrere Brüche werden addiert, indem man die Nenner durch Kürzen oder Erweitern gleich macht. Anschließend werden die Zähler addiert oder subtrahiert und der gemeinsame Nenner behalten.
Das Lernvideo Brüche addieren wurde für eine interaktive Unterrichtsstunde oder auch Flipped Classroom Stunde erstellt.
Beispiel 1:
Der gemeinsame Nenner von 2 und 3 ist 6. Das ist auch das kleinste gemeinsame Vielfache kgV von 2 und 3.
$\frac{1}{2}+ \frac{1}{3} = \frac{3}{6} + \frac{2}{6} = \frac{3+2}{6}=\frac{5}{6}$
Beispiel 2:
$\frac{3}{8} +\frac{1}{4} + \frac{1}{3} = \frac{9}{24} + \frac{6}{24}+\frac{8}{24}= \frac{9+6+8}{24}=\frac{23}{24} $
Aufgaben zur Addition von Brüchen
1. Aufgabe - einfache Brüche, nur 2 Summanden
a) $\frac{3}{8}+\frac{1}{4}$
b) $\frac{2}{7}+\frac{3}{5}$
c) $\frac{1}{5}+\frac{3}{4}$
d) $\frac{2}{9}+\frac{2}{3}$
e) $\frac{5}{7}+\frac{1}{3}$
f) $\frac{2}{9}+\frac{3}{10}$
g) $\frac{1}{8}+\frac{3}{7}$
h) $\frac{7}{10}+\frac{4}{5}$
Viele weitere solcher Aufgaben zur Bruchrechnung findet ihr im Übungsheft einfache Bruchrechnung!
Brüche multiplizieren
dieses Kapitel wird noch erstellt!
Brüche dividieren
dieses Kapitel wird noch erstellt!
Doppel- und Mehrfachbrüche - die Königsdisziplin!
dieses Kapitel wird noch erstellt!