Der Satz des Pythagoras - Definition - Herleitung
Der Satz des Pythagoras in Worten
Die Summe der Flächeninhalte der Kathetenquadrate ist gleich dem Flächeninhalt des Hypotenusenquadrates.

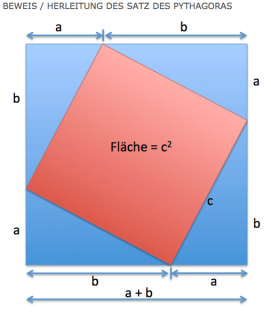
Beweis / Herleitung des Satz des Pythagoras

Im obigen Bild ist ein kleines Quadrat in ein großes Quadrat eingefügt. Beachte, dass 4 gleich große Dreiecke an den Ecken entstehen.
Mit dieser Erkenntnis können wir den Satz des Pythagoras herleiten:
Fläche des großen Quadrats:
(a+b)2=a2+2ab+b2
Als Summe des kleinen roten Quadrats + 4 Dreiecke (blau):
c2+4⋅(12a⋅b)
Wir setzen beide Flächen gleich.
a2+2ab+b2=c2+4⋅12a⋅b
a2+2ab+b2=c2+2ab
und wir erhalten damit den Satz des Pythagoras:
a2+b2=c2
Beachte: bezeichnet man die Seiten im rechtwinkligen Dreieck anders, muss man den Satz des Pythagoras auch umstellen. Die längste Seite (das ist die Hypothenuse) steht immer im Quadrat auf der einen Seite und die anderen beiden Seiten (nennt man Katheten) stehen jeweils im Quadrat auf der anderen Seite!
Der Satz des Pythagoras anschaulich
Dieses Bild wird immer im Zusammenhang mit Pythagoras gezeigt!