Zweiersystem Klasse 5 – Einfach erklärt

Was ist das Zweiersystem?

Das Zweiersystem, auch als Binärsystem bekannt, ist ein Zahlensystem, das nur zwei Ziffern verwendet: 0 und 1. Während wir im Alltag das Dezimalsystem mit den Ziffern 0 bis 9 nutzen, arbeiten Computer mit dem Zweiersystem. Das liegt daran, dass Computer nur zwischen zwei Zuständen unterscheiden können: an (1) und aus (0). In Klasse 5 lernen Schülerinnen und Schüler, wie man im Binärsystem rechnet und welche Bedeutung dieses System in der Informatik hat.

Wie funktioniert das Rechnen im Zweiersystem?

Das Rechnen im Zweiersystem ist im Grunde ähnlich wie im Dezimalsystem, aber anstelle von zehn Ziffern gibt es nur zwei. Die Stellenwerte sind Potenzen von 2. Die erste Stelle rechts hat den Wert 1 (2^0), die zweite Stelle den Wert 2 (2^1), die dritte Stelle den Wert 4 (2^2) und so weiter. Um eine Zahl wie 1011 im Binärsystem in das Dezimalsystem umzuwandeln, addiert man die Potenzen von 2 an den Stellen, an denen eine 1 steht. In diesem Fall ist 1011 = 1*2^3 + 0*2^2 + 1*2^1 + 1*2^0 = 8 + 2 + 1 = 11 im Dezimalsystem.

Beispiele und Anwendungen des Zweiersystems

Das Zweiersystem findet vor allem in der Informatik und Technik Anwendung. Alle Daten, die von Computern verarbeitet werden, werden in Form von 0 und 1 gespeichert. Ein bekanntes Beispiel ist die Speicherung von Texten, Bildern und Musik auf einem Computer. Wenn du in der Schule Programmieren lernst, wirst du ebenfalls auf das Binärsystem stoßen. Ein einfaches Beispiel wäre die Zahl 5, die im Binärsystem als 101 dargestellt wird. Solche Umrechnungen von Dezimalzahlen ins Binärsystem sind wichtige Übungen im Unterricht der Klasse 5.

Übungen zum Zweiersystem für Klasse 5

Um das Zweiersystem besser zu verstehen, ist es hilfreich, viele Übungen durchzuführen. Ein Beispiel wäre: Wandle die Zahl 13 ins Zweiersystem um. Die Lösung ist 1101, da 13 = 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0. Andere typische Aufgaben umfassen das Addieren und Subtrahieren von Binärzahlen, das Umrechnen von größeren Dezimalzahlen oder das Vergleichen von Werten im Binärsystem. Durch solche Übungen werden die Grundlagen gefestigt und der Umgang mit dem Binärsystem wird zur Routine.

Beachte auch unseren Zweiersystem - Umrechner als eigene App:

Der Zweiersystem-Rechner online

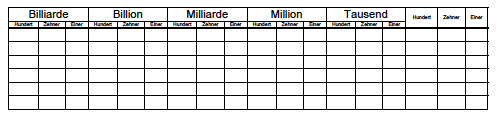
Wir identifizieren Zahlen im Stellenwertsystem

indem wir Einer, Zehner, Hunderter, Tausender, Zehntausender und Hunderttausender in einer Tabelle eintragen.

Wir schreiben Zahlen als Summe der Einer, Zehner und Hunderter

z.B. 398 = 8 + 90 + 300 

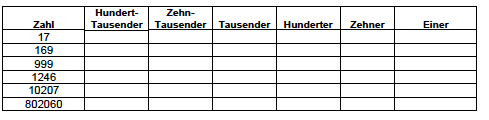
Wir schreiben Zahlen die als Wort genannt sind in die Stellenwerttafel:

z.B.:

a) Einhundertsiebzehn

b) Dreihundertachtundvierzigtausendneunhundertacht

c) Fünf Millionen vierhundertneun Tausendsiebenhundertachtundzwanzig

Wir übertragen Zahlen vom Zweiersystem ins Zehnersystem und umgekehrt:

Schreibe im Dezimalsystem a) 11011 b) 01101 c) 11110111 d) 010111 e) 1100011

Schreibe im Binärsystem a) 47 b) 66 c) 100 d) 150 e) 247 f) 200

Addition im Zweiersystem und Übertragung der Zahlen ins Zehnersystem

a)

   1 1 0 0 1

+ 1 1 1 1 0

b)

   1 1 0 1 0 1

+ 1 0 1 1 1 1