Die Tangentengleichung - ein wichtiges Thema in der Differenzialrechnung

Wozu benötigt man die Tangentengleichung?

Versteht man den Verlauf des Graphen einer Funktion als Bahnkurve einer Bewegung, so würde sich ich die Bewegung in Richtung der Tangente an einer Stelle fortsetzen, wenn dort die Bedingungen für die bisherige Bewegung nicht mehr gelten. Was heißt das:

• Im Fall einer Kurvenfahrt mit dem Auto setzt sich die Bewegung tangential fort, wenn die Reibung plötzlich nicht mehr vorhanden ist. Kurz: Fährt man zu schnell in eine Kurve, fliegt man tangential aus der Kurve.
• Auf einer Skifllugschanze verläßt man zunächst die Bahn tangential und gäbe es keine Erdanziehungskraft, die für eine Parabelförmige Bahnkurve sorgt, würde man tangential weiter fliegen.
• ...

Die Herleitung der Tangentengleichung der Tangente in einem Punkt P auf der Funktion f(x).

Ich leite die Formel her und rechne eine Beispielaufgabe und eine Schüler Übungsaufgabe.

In dieser Einheit (2 Unterrichtstunden) leiten wir die Gleichung für die Tangente an einer Funktion im Punkt P her und rechnen einige Übungsaufgaben.

Die allgemeine Gleichung einer linearen Funktion sollte bekannt sein. Falls hier Wiederholungsbedarf besteht, einfach in meinem Skript einmal nachlesen.

Die Tangentengleichung einer Funktion f an der Stelle x0 lautet:

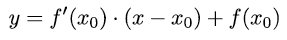
Anschließend rechnen wir eine Beispielaufgabe:

Gegeben sei die Funktion f(x): 

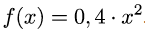
Bestimme die Steigung im Punkt P(-2/f(-2)). Wie lautet die Gleichung für die Tangente an f(x) , die durch den Punkt P verläuft?

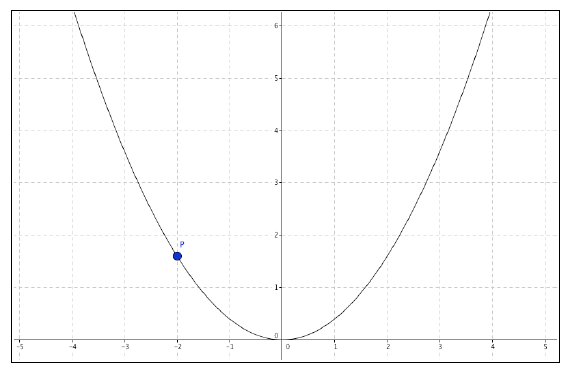
Die Berechnung erfolgt mit Hilfe der h-Methode zur Berechnung des Differenzenquotienten:

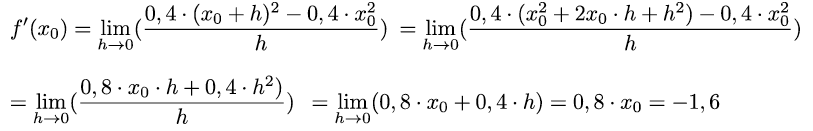
Nach Berechnung der Steigung bestimmen wir den y-Achsenabschnitt

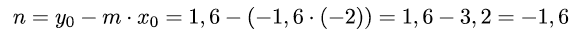
und stellen die Tangentengleichung mit der nun bekannten Steigung und dem y-Achsenabschnitt auf:

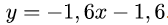
Herleitung, Beispiele, Schülerarbeitsblatt