Wie viele primzahlen bis 100 gibt es - Schnell erklärt
Bis 100 gibt es 25 Primzahlen.
Eine Primzahl ist eine natürliche Zahl, die nur durch 1 und sich selbst teilbar ist.
Die Primzahlen bis 100 lauten: 2 , 3 , 5 , 7 , 11 , 13 , 17 , 19 , 23 , 29 , 31 , 37 , 41 , 43 , 47 , 53 , 59 , 61 , 67 , 71 , 73 , 79 , 83 , 89 , 97
Methode zur Bestimmung der Primzahlen bis 100 Um alle Primzahlen bis 100 zu finden, verwendet man häufig den Sieb des Eratosthenes. Dies ist eine effiziente Methode, um Primzahlen bis zu einer bestimmten Grenze zu ermitteln. Hier ist eine Schritt-für-Schritt-Anleitung: Liste erstellen: Erstellen Sie eine Liste aller Zahlen von 2 bis 100. Kleinste Zahl auswählen: Beginnen Sie bei der kleinsten Zahl, die noch nicht durchgestrichen ist (zunächst die 2). Diese Zahl ist eine Primzahl. Vielfache streichen: Streichen Sie alle Vielfachen dieser Primzahl aus der Liste, da diese keine Primzahlen sind. Nächste Zahl auswählen: Gehen Sie zur nächsten Zahl in der Liste, die noch nicht durchgestrichen ist (in diesem Fall die 3), und wiederholen Sie den Prozess. Fortsetzen: Fahren Sie fort, bis Sie alle Zahlen bis zur Quadratwurzel der höchsten Zahl (hier etwa 10) überprüft haben. Die verbleibenden Zahlen in der Liste sind Primzahlen. Mit dieser Methode findet man alle 25 Primzahlen bis 100 auf effiziente Weise.
Wie viele Primzahlen gibt es überhaupt?
Es gibt unendlich viele Primzahlen. Das bedeutet, dass wir niemals alle Primzahlen aufschreiben können, weil es immer eine weitere Primzahl gibt, egal wie weit wir zählen.
Einfache Erklärung, warum es unendlich viele Primzahlen gibt
Man kann dies mit einem bekannten mathematischen Argument erklären, das auf den griechischen Mathematiker Euklid zurückgeht. Die Idee ist recht einfach und geht so:
- Annahme: Stellen wir uns vor, es gäbe nur eine begrenzte Anzahl von Primzahlen. Angenommen, die größten Primzahlen wären \( p_1, p_2, p_3, \ldots, p_n \).
- Neue Zahl bilden: Jetzt nehmen wir alle diese Primzahlen und multiplizieren sie miteinander. Danach addieren wir 1 dazu. Die neue Zahl wäre: \[ N = (p_1 \times p_2 \times p_3 \times \ldots \times p_n) + 1 \]
- Unteilbarkeit: Diese neue Zahl \( N \) ist nicht durch irgendeine der Primzahlen \( p_1, p_2, \ldots, p_n \) teilbar. Denn wenn man \( N \) durch eine dieser Primzahlen teilt, bleibt immer ein Rest von 1 übrig.
- Schlussfolgerung: Da \( N \) also durch keine der Primzahlen teilbar ist, muss entweder \( N \) selbst eine neue Primzahl sein oder durch andere Primzahlen teilbar, die nicht in unserer Liste standen. Das bedeutet, dass unsere Annahme, es gäbe nur endlich viele Primzahlen, falsch ist.
Ergebnis
Es gibt also unendlich viele Primzahlen, weil wir immer eine weitere finden können, egal wie viele wir schon kennen.
Primzahlen bis 100 - Alle Zahlen und Erklärungen
 In der heutigen digitalen Welt, in der Persönlichkeitsrechte und Datensicherheit oberste Priorität haben, spielen Primzahlen eine entscheidende Rolle bei der Verschlüsselung von Daten. Aber was genau macht Primzahlen so besonders und wie tragen sie dazu bei, unsere Daten sicher zu halten?
In der heutigen digitalen Welt, in der Persönlichkeitsrechte und Datensicherheit oberste Priorität haben, spielen Primzahlen eine entscheidende Rolle bei der Verschlüsselung von Daten. Aber was genau macht Primzahlen so besonders und wie tragen sie dazu bei, unsere Daten sicher zu halten?
Die Geheimnisse der Primzahlenverschlüsselung werden in diesem Artikel enthüllt. Erfahre, warum Primzahlen als ultimative Schlüssel für sichere Kommunikation gelten und wie sie es Mathematikern und Informatikern ermöglichen, komplexe Verschlüsselungsverfahren zu entwickeln.
Die einzigartige Eigenschaft von Primzahlen liegt in ihrer Unzerlegbarkeit - sie können nur durch 1 und sich selbst ohne Rest geteilt werden. Diese Eigenschaft bildet die Grundlage für kryptographische Systeme wie RSA, die von Unternehmen und Regierungen auf der ganzen Welt eingesetzt werden.
Tauche ein in die faszinierende Welt der Primzahlenverschlüsselung und lerne, wie diese unsichtbaren Helden der Datensicherheit unseren digitalen Alltag schützen.
Was sind Primzahlen?
Primzahlen sind eine besondere Gruppe von natürlichen Zahlen, die nur durch 1 und sich selbst teilbar sind. Das bedeutet, sie haben genau zwei positive Teiler. Eine der bekanntesten Primzahlen ist 2, die einzige gerade Primzahl. Jede andere gerade Zahl kann durch 2 geteilt werden, was sie von den Primzahlen unterscheidet. Primzahlen spielen eine zentrale Rolle in der Zahlentheorie und werden in vielen Bereichen der Mathematik und Technik verwendet, wie etwa in der Kryptografie.
Primzahlen sind für die Verschlüsselung wichtig, insbesondere in der modernen Kryptographie, aus zwei Hauptgründen:
Die Liste: alle Primzahlen bis 100
Jede Zahl, die keine Primzahl ist, kann man in Faktoren zerlegen, bis es nicht mehr weiter geht. Diese Faktoren heißen dann Primfaktoren. Eine Zahl automatisch in Primfaktoren zerlegen kannst du mit unserem online-Primfaktor-Zerlegungsprogramm!
Die ersten 100 Primzahlen solltest du kennen:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101 ...
Eine Liste "aller" Primzahlen findest du z.B. hier:
Liste aller Primzahlen bis 100 000 bei Wikipedia
(Das ist immer eine Frage bis zu welcher Zahl. Supercomputer berechnen heute noch immer weitere immer größere Primzahlen!)
Der Primzahlen Rechner - Berechne alle Primzahlen bis 100 oder mehr von bis selbst.
Mit unserem Primzahlen Rechner kannst du beliebige Primzahlen selbst berechnen lassen. Gib einfach die Startzahl zur Primzahlenberechnung ein und gib die Endzahl ein, bis zu der du die Primzahlen haben möchtest. Der Primzahlenrechner rechnet dir alle Zahlen aus!
Primzahlen berechnen mit dem Sieb des Eratosthenes
Das Sieb des Eratosthenes ist eine einfache Methode, um Primzahlen zu finden. Eine Primzahl ist eine Zahl, die nur durch 1 und sich selbst teilbar ist, wie 2, 3 oder 5. Hier erfährst du, wie das Sieb des Eratosthenes funktioniert:
1. Schritt: Schreibe alle Zahlen von 2 bis zu einer gewünschten Zahl auf, z. B. von 2 bis 30. Die Zahl 1 wird nicht berücksichtigt, weil sie keine Primzahl ist.
2. Schritt: Beginne mit der ersten Zahl, die 2 ist. Sie ist eine Primzahl. Nun streiche alle Vielfachen von 2 (also 4, 6, 8, 10 usw.), da diese keine Primzahlen sein können, weil sie durch 2 teilbar sind.
3. Schritt: Gehe zur nächsten nicht gestrichenen Zahl, die 3 ist. Sie ist eine Primzahl. Streiche dann alle Vielfachen von 3 (also 6, 9, 12, 15 usw.).
4. Schritt: Fahre auf diese Weise mit der nächsten nicht gestrichenen Zahl fort, die 5 ist. Sie ist ebenfalls eine Primzahl. Streiche alle Vielfachen von 5 (also 10, 15, 20 usw.).
5. Schritt: Wiederhole diesen Vorgang, bis du bei einer Zahl angekommen bist, deren Quadrat größer ist als die letzte Zahl in deiner Liste.
Am Ende bleiben nur die Primzahlen übrig, da alle anderen Zahlen durch eine kleinere Zahl teilbar sind. So hast du alle Primzahlen in einem bestimmten Bereich gefunden!
Probiere das Sieb des Eratosthenes aus, indem du unsere Hundertertabelle auf der nächsten Folie verwendest!
Alle Primzahlen bis 20
Hier siehst du alle Primzahlen bis 20, die Folien kannst du downloaden, klicke einfach auf das Bild.n. Ebenso befindet sich der HTML-Code für den Primzahl Rechner in der Datei.
Alle Primzahlen bis 40
Hier siehst du alle Primzahlen bis 40, die Folien kannst du downloaden, klicke einfach auf das Bild.
Alle Primzahlen bis 50
Hier siehst du alle Primzahlen bis 50, die Folien kannst du downloaden, klicke einfach auf das Bild.
Alle Primzahlen bis 60
Hier siehst du alle Primzahlen bis 60, die Folien kannst du downloaden, klicke einfach auf das Bild..
Das Skript mit allen Folien und dem HTML-Code für den Primzahlen Rechner kannst du hier kostenlos Downloaden!
Matheaufgaben zu Primzahlen mit Lösungen
Es gibt viele Plattformen, auf denen Sie Matheaufgaben zu Primzahlen lösen können. Mit Tools wie ChatGPT können Sie Aufgaben zu Primzahlen schnell und effektiv lösen lassen. Zum Beispiel:
- Welche Primzahlen gibt es zwischen 50 und 100?
- Wie viele Primzahlen gibt es zwischen 1 und 100?
- Erklären Sie das Sieb des Eratosthenes.
- Warum ist 1 keine Primzahl?
- Was ist die größte Primzahl unter 100?
Wenn dir das Programm zur Primzahlberechnung gefällt, empfehle uns einfach weiter, teile die Seite auf Facebook oder Instagram.
Einführung in die Primzahlverschlüsselung
Primzahlen sind natürliche Zahlen, die größer als 1 sind und nur durch 1 und sich selbst ohne Rest teilbar sind. Sie sind die Bausteine, aus denen komplexe Verschlüsselungsalgorithmen aufgebaut werden. Ihre Einzigartigkeit und mathematischen Eigenschaften machen sie zu den perfekten Kandidaten für die Verschlüsselung von Daten.
Ein wichtiger Aspekt der Primzahlverschlüsselung ist der Primfaktorzerlegungsalgorithmus. Dieser Algorithmus ermöglicht es uns, eine große Zahl in ihre Primfaktoren zu zerlegen, was die Grundlage für die Verschlüsselung und Entschlüsselung von Daten bildet. Durch die Verwendung von Primzahlen als Schlüssel können wir sicherstellen, dass die verschlüsselten Daten nur von autorisierten Personen entschlüsselt werden können.
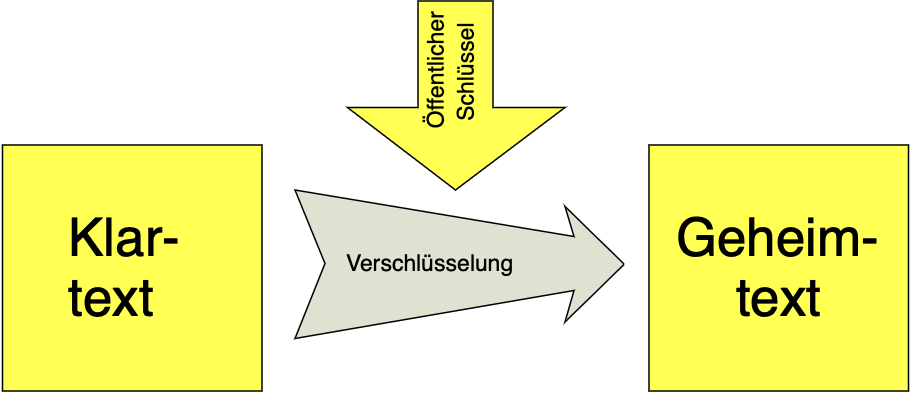
Die Primzahlverschlüsselung ist ein komplexer Prozess, der auf mathematischen Prinzipien basiert. Es erfordert spezielle Algorithmen und Berechnungen, um die Sicherheit der Daten zu gewährleisten. Durch die Verwendung von Primzahlen als Grundlage für die Verschlüsselung können wir sicherstellen, dass unsere Daten vor unbefugtem Zugriff geschützt sind.
Prinzip der Verschlüsselung, Quelle: Wikipedia.org
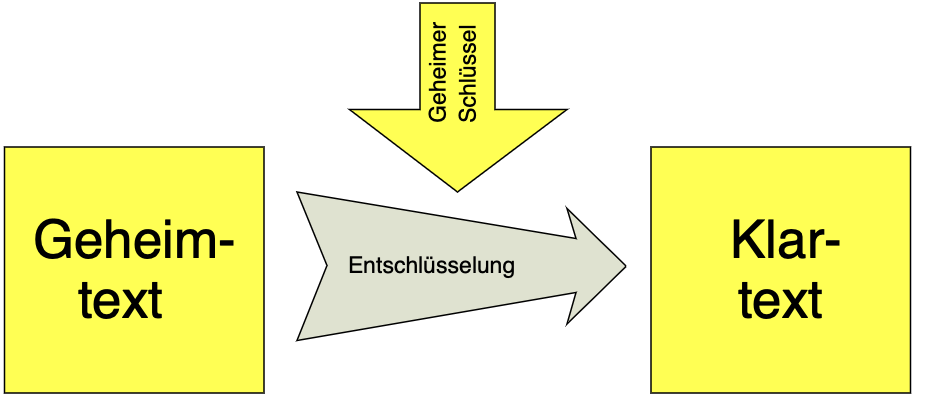
Prinzip der Entschlüsselung, Quelle: Wikipedia.org
Warum sind Primzahlen für die Verschlüsselung wichtig?
Die Verwendung von Primzahlen als Grundlage für die Verschlüsselung bietet verschiedene Vorteile. Einer der wichtigsten Vorteile ist die mathematische Komplexität der Primzahlverschlüsselung. Durch die Verwendung von Primzahlen als Schlüssel können wir sicherstellen, dass die Verschlüsselung robust und sicher ist.
Ein weiterer Vorteil der Primzahlverschlüsselung ist ihre Wechselwirkung mit anderen mathematischen Operationen. Durch die Kombination von Primzahlen mit anderen mathematischen Prinzipien können wir komplexe Verschlüsselungssysteme entwickeln, die eine hohe Sicherheit bieten.
Darüber hinaus ist die Primzahlverschlüsselung aufgrund ihrer mathematischen Eigenschaften effizient und schnell. Die Berechnungen, die für die Verschlüsselung und Entschlüsselung von Daten erforderlich sind, können mit Hilfe von Primzahlen effizient durchgeführt werden, was zu einer schnellen und effektiven Sicherung der Daten führt.
Der Prozess der Primzahlverschlüsselung
Die Primzahlverschlüsselung hat viele Anwendungen in der Datensicherheit. Ein bekanntes Beispiel ist die RSA-Verschlüsselung, die auf Primzahlen basiert und weit verbreitet ist. Die RSA-Verschlüsselung wird von Unternehmen und Regierungen für die sichere Kommunikation und den Schutz sensibler Daten verwendet.
Ein weiteres Anwendungsgebiet der Primzahlverschlüsselung ist die sichere Übertragung von Daten über unsichere Netzwerke wie das Internet. Durch die Verwendung von Primzahlen als Grundlage für die Verschlüsselung können wir sicherstellen, dass die Daten während der Übertragung vor unbefugtem Zugriff geschützt sind.
Darüber hinaus wird die Primzahlverschlüsselung auch in der digitalen Signatur verwendet. Durch die Verwendung von Primzahlen können digitale Signaturen erstellt werden, die die Authentizität und Integrität von digitalen Dokumenten gewährleisten.
Vorteile der Primzahlverschlüsselung
Obwohl die Primzahlverschlüsselung eine effektive Methode zur Sicherung von Daten ist, gibt es auch Herausforderungen und Grenzen. Eine der Herausforderungen besteht darin, geeignete Primzahlen zu finden, die für die Verschlüsselung verwendet werden können. Die Auswahl geeigneter Primzahlen erfordert spezielle Algorithmen und Berechnungen.
Ein weiteres Problem besteht darin, dass die Sicherheit der Primzahlverschlüsselung von der Größe der verwendeten Primzahlen abhängt. Je größer die Primzahlen sind, desto sicherer ist die Verschlüsselung. Es ist wichtig, Primzahlen mit ausreichender Größe zu wählen, um eine effektive Sicherheit zu gewährleisten.
Darüber hinaus können auch technische Faktoren wie die Rechenleistung und die Verfügbarkeit von Ressourcen die Wirksamkeit der Primzahlverschlüsselung beeinflussen. Es ist wichtig, die technischen Aspekte bei der Implementierung von Primzahlverschlüsselungsalgorithmen zu berücksichtigen.
Anwendungen der Primzahlverschlüsselung in der Datensicherheit
Es gibt verschiedene Algorithmen, die für die Primzahlverschlüsselung verwendet werden. Einer der bekanntesten Algorithmen ist der RSA-Algorithmus, der auf Primzahlen basiert. Der RSA-Algorithmus ermöglicht eine sichere Verschlüsselung und Entschlüsselung von Daten und wird häufig in der Praxis eingesetzt.
Weitere und detaillierte Infos zu dem RSA-Verfahren findest du bei Wikipedia.
Ein weiterer Algorithmus ist der Diffie-Hellman-Schlüsselaustausch, der ebenfalls auf Primzahlen basiert. Der Diffie-Hellman-Schlüsselaustausch ermöglicht es zwei Parteien, einen gemeinsamen Schlüssel zu vereinbaren, ohne ihn tatsächlich zu übertragen. Dieser Schlüssel kann dann für die Verschlüsselung und Entschlüsselung von Daten verwendet werden.
Darüber hinaus gibt es noch andere Algorithmen wie den Elgamal-Algorithmus und den DSA-Algorithmus, die auf Primzahlen basieren und in der Praxis eingesetzt werden. Jeder dieser Algorithmen hat seine eigenen Stärken und Anwendungsgebiete.
Herausforderungen und Grenzen der Primzahlverschlüsselung
Die Primzahlverschlüsselung spielt eine wichtige Rolle in unserem täglichen Leben, auch wenn wir uns dessen oft nicht bewusst sind. Viele unserer alltäglichen Aktivitäten wie das Online-Banking, das Einkaufen im Internet und das Versenden von E-Mails werden durch die Primzahlverschlüsselung geschützt.
Wenn wir unsere Kreditkarteninformationen online eingeben, verwenden die meisten Websites eine sichere Verbindung, die auf Primzahlverschlüsselung basiert, um sicherzustellen, dass unsere Daten während der Übertragung geschützt sind. Ebenso werden E-Mails häufig mit Hilfe von Primzahlverschlüsselung verschlüsselt, um sicherzustellen, dass sie nur vom beabsichtigten Empfänger gelesen werden können.
Darüber hinaus werden auch mobilfunkbasierte Kommunikationssysteme wie GSM und LTE durch Primzahlverschlüsselung geschützt. Dies gewährleistet die Sicherheit der Kommunikation und schützt vor unbefugtem Zugriff auf unsere persönlichen Daten.
Algorithmen zur Primzahlverschlüsselung
Die Primzahlverschlüsselung ist ein sich ständig weiterentwickelndes Gebiet der Kryptographie. Forscher und Entwickler arbeiten ständig an neuen und verbesserten Algorithmen und Techniken, um die Sicherheit von Primzahlverschlüsselung weiter zu verbessern.
Eine vielversprechende Entwicklung ist die Verwendung von Quantencomputern in der Primzahlverschlüsselung. Quantencomputer haben das Potenzial, die Primzahlverschlüsselung zu brechen und neue Verschlüsselungsmethoden erforderlich zu machen. Daher wird intensiv an Quantenverschlüsselungsalgorithmen gearbeitet, die gegenüber Quantencomputern sicher sind.
Darüber hinaus werden auch andere mathematische Konzepte wie elliptische Kurven und Gitter-basierte Verschlüsselung erforscht, um die Sicherheit und Effizienz der Primzahlverschlüsselung weiter zu verbessern.
Primzahlverschlüsselung im täglichen Leben
Die Primzahlverschlüsselung spielt eine entscheidende Rolle bei der Sicherung unserer Daten in der digitalen Welt. Primzahlen sind einzigartig und mathematisch komplex, was sie zu idealen Kandidaten für die Verschlüsselung macht. Die Verwendung von Primzahlen als Grundlage für die Verschlüsselung ermöglicht sichere Kommunikation und den Schutz sensibler Daten.
Trotz einiger Herausforderungen und Grenzen bleibt die Primzahlverschlüsselung eine der effektivsten Methoden, um Daten sicher zu verschlüsseln. Mit ständigen Fortschritten in der Kryptographie und der Entwicklung neuer Algorithmen wird die Primzahlverschlüsselung auch in Zukunft eine wichtige Rolle bei der Sicherung unserer digitalen Leben spielen.
Schlussfolgerung
Obwohl Primzahlverschlüsselung ein wichtiger Bestandteil der Datensicherheit ist, gibt es immer noch Raum für Verbesserungen. Eines der größten Probleme bei der Primzahlverschlüsselung ist, dass sie anfällig für Quantencomputer ist.
Quantencomputer können große Zahlen in kürzester Zeit faktorisieren und somit die Verschlüsselung von Primzahlen knacken. Die zukünftige Entwicklung der Primzahlverschlüsselung wird voraussichtlich darauf abzielen, Quantencomputer-resistente Verschlüsselungsalgorithmen zu entwickeln.
Ein vielversprechender Ansatz ist die Verwendung von Post-Quanten-Kryptographie, die sich auf die Verwendung von mathematischen Problemen konzentriert, die selbst mit Quantencomputern nicht gelöst werden können.
Eine andere Möglichkeit besteht darin, die Verschlüsselung von Primzahlen durch die Verwendung von mehreren Primzahlen zu verbessern. Dies würde es schwieriger machen, die Verschlüsselung zu knacken, da eine höhere Anzahl von Primzahlen ein höheres Sicherheitsniveau bietet.
Übungen und Aufgaben zu Primzahlen
Wenn Sie Primzahlen besser verstehen möchten, können Sie verschiedene Übungen und Aufgaben zu diesem Thema lösen. Es gibt viele Webseiten, die Matheaufgaben mit Lösungen anbieten. Eine gute Möglichkeit, mehr über Primzahlen und deren Anwendung zu lernen, ist es, Aufgaben zu lösen und die Lösungen Schritt für Schritt nachzuvollziehen. Hier sind einige Webseiten, die Ihnen dabei helfen können:





