Bedeutung der lokalen Änderungsrate
Betrachten wir die Definition der Geschwindigkeit in der Physik. Bei einer gleichförmigen geradlinigen Bewegung gilt:
![]()
Handelt es sich um eine allgemeine Bewegung und die Änderungsrate der Strecke je Zeit ist nicht konstant, so ist ebenfalls die Geschwindigkeit nicht konstant, sondern diese ergibt sich durch die lokale Änderungsrate an einer bestimmten Stelle x. Dies haben wir in der Differentialrechnung als Ableitung kennen gelernt. Die Momentangeschwindigkeit ergibt sich an der Stelle x durch die Bildung des Grenzwertes und auf diese Weise wurde die 1. Ableitung definiert:
![]()
Die erste Ableitung der Strecke nach der Zeit.
Da wir in der Mathematik die x-Richtung betrachten anstelle der Strecke s ist die obige Gleichung gleichbedeutend mit:
![]()
Bei konstanter Geschwindigkeit kann auf den zurückgelegten Weg geschlossen werden, indem wir die Gleichung einfach umstellen:
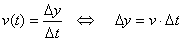
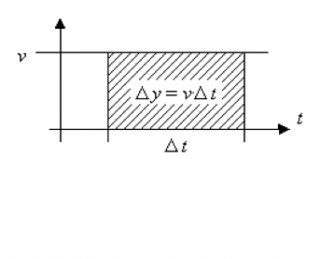
Da die Geschwindigkeit v konstant ist, ist diese Funktion eine konstante Funktion. Dies sehen wir im Weg-Zeit Diagramm:
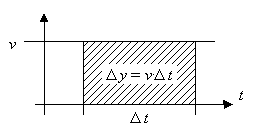
Die zurückgelegte Strecke ist die Fläche unter der Parallelen zur t-Achse. Das Rechteck hat die Fläche:
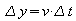
(siehe Bild, schraffierte Fläche).