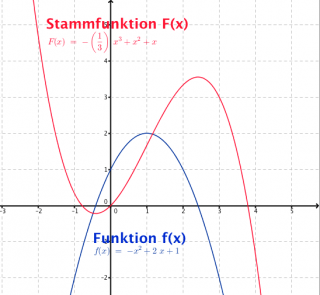
Definiton Stammfunktion
Jede Funktion F, für die gilt: F’(x) = f(x) heißt Stammfunktion von f.
Dabei muss f(x) differenzierbar sein!
Das Auffinden einer Stammfunktion heißt Integration.
Eine Stammfunktion F einer Funktion f(x) ist bis auf eine Integrationskonstante C genau bestimmt. Das wird deutlich, wenn man die Stammfunktion ableitet. Denn bei diesem Vorgang verschwindet die Konstante C.
Es gibt folglich eine unbestimmte Menge an Stammfunktionen zu einer Funktion f(x). Daher nennt man die Menge der Stammfunktionen zu einer Funktion f(x) auch unbestimmtes Integral.


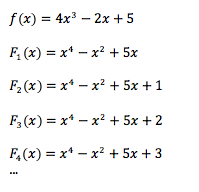
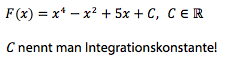
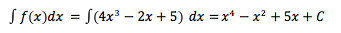
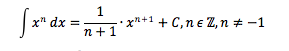
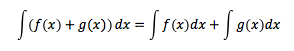
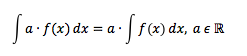
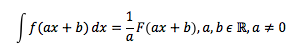
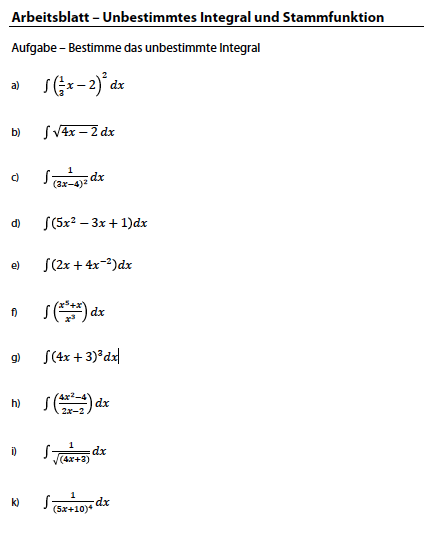 Arbeitsblatt zu unbestimmten Integralen
Arbeitsblatt zu unbestimmten Integralen